Moving Average Model
Moving average model of order 1
The moving average (MA) model is a linear combination of $Z$’s. The MA(1) model is given by:
$$ X_t = \mu + Z_t + \theta Z_{t-1} $$
where $\mu$ is the overall mean, $\theta$ is a moving average coefficient, and $Z_t \overset{i.i.d.}{\sim} N(0, \sigma^2)$.
Note that many books use $-\theta$ in the formula, but we’re following R’s convention with the $+\theta$.
Mean and variance
The expectation is
$$ E(X_t) = \mu + E(Z_t) + \theta E(Z_{t-1}) = \mu $$
Setting $\mu = 0$, the variance is
$$ Var(X_t) = Var(Z_t + \theta Z_{t-1}) = Var(Z_t) + \theta^2 Var(Z_{t-1}) = (1 + \theta^2)\sigma^2 $$
Autocovariance and autocorrelation
The autocovariance function of lag 1 is
$$ \begin{aligned} \gamma_X(1) &= Cov(X_t, X_{t-1}) \\ &= Cov(Z_t + \theta Z_{t-1}, X_{t-1}) \\ &= Cov(Z_t, X_{t-1}) + \theta Cov(Z_{t-1}, X_{t-1}) \\ &= \theta Cov(Z_{t-1}, Z_{t-1} + \theta Z_{t-2}) \\ &= \theta \left[ Cov(Z_{t-1}, Z_{t-1}) + \theta Cov(Z_{t-1}, Z_{t-2}) \right] \\ &= \theta \sigma^2 \end{aligned} $$
Thus the autocorrelation of lag 1 is
$$ \rho_X(1) = \frac{\gamma_X(1)}{\gamma_X(0)} = \frac{\theta}{1 + \theta^2} $$
For time lags of 2 and above,
$$ \begin{aligned} \gamma_X(k) &= Cov(X_t, X_{t-k}) \\ &= Cov(Z_t + \theta Z_{t-1}, X_{t-k}) \\ &= Cov(Z_t, X_{t-k}) + \theta Cov(Z_{t-1}, X_{t-k}) \\ &= 0, \quad k = 2, 3, \cdots \end{aligned} $$
which means
$$ \rho_X(k) = 0,\quad k = 2, 3, \cdots $$
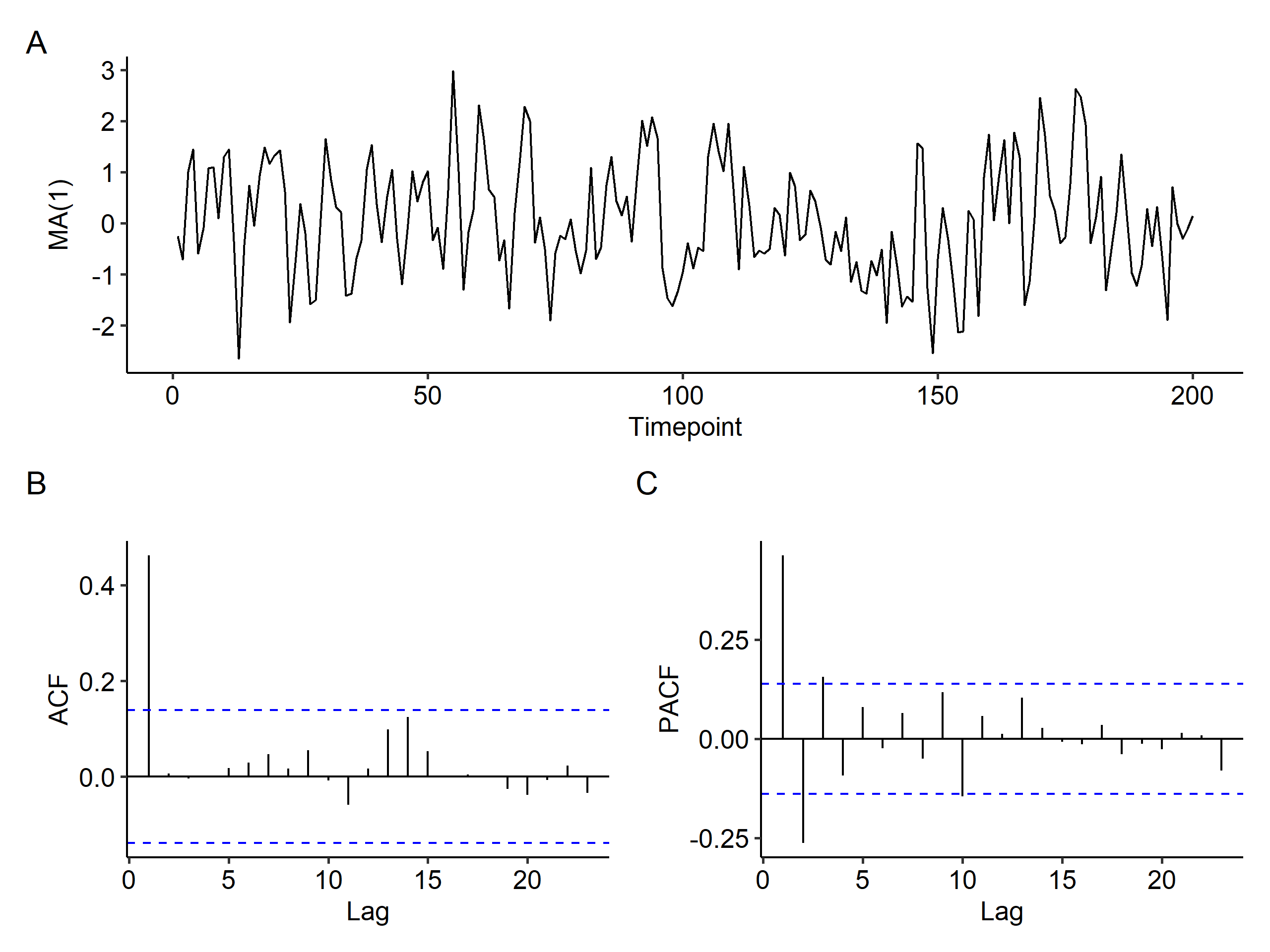
A sample ACF with significant autocorrelation only at lag 1 is an indicator of a potential MA(1) model.
Partial autocorrelation
For the MA(1) model, the PACF is
$$ \phi_{00} = 1, \phi_{11} = \frac{\theta}{1 + \theta^2} = \rho(1), \phi_{kk} = \frac{\theta^k(1-\theta^2)}{1 - \theta^{2(k+1)}} \text{ for } k > 1 $$
The PACF od MA(1) tails off after lag 1.
Simulation in R
We can use the arima.sim() function to simulate the MA model, specifying the model parameter as list(ma = theta). Of course we can also write our own function to generate a series manually:
| |
Here’s an example of a simulated MA(1) series with $n=200$ timepoints1. We can see the tail off pattern in the ACF and the cut off after lag 1 in the PACF.
Moving average model of order $q$
The model is
$$ X_t = \mu + Z_t + \theta_1 Z_{t-1} + \theta_2 Z_{t-2} + \cdots + \theta_q Z_{t-q} $$
where the $\theta_j$’s are moving average coefficients and $Z_t$ is $WN(0, \sigma^2)$.
Mean and variance
The terms are all independent, so we don’t have to worry about covariance terms when finding the variance:
$$ E(X_t) = \mu, Var(X_t) = (1 + \theta_1^2 + \theta_2^2 + \cdots + \theta_q^2)\sigma^2 $$
MA(q) is always stationary.
Autocovariance and autocorrelation
The autocovariance for lag 1 is:
$$ \begin{aligned} \gamma_X(1) = &= E\left[(Z_t + \theta_1 Z_{t-1} + \cdots + \theta_q Z_{t-q})(Z_{t-1} + \theta_1 Z_{t-2} + \cdots + \theta_q Z_{t-1-q}) \right] \\ &= (\theta_1 + \theta_2 \theta_1 + \theta_3 \theta_2 + \cdots + \theta_q \theta_{q-1})\sigma^2 \end{aligned} $$
The autocovariance function for lag $k$ is:
$$ \begin{aligned} \gamma_X(1) = &= E\left[(Z_t + \theta_1 Z_{t-1} + \cdots + \theta_q Z_{t-q})(Z_{t-k} + \theta_1 Z_{t-k-1} + \cdots + \theta_q Z_{t-k-q}) \right] \\ &= \begin{cases} (\theta_k + \theta_{k+1} \theta_1 + \theta_{k+2} \theta_2 + \cdots + \theta_q \theta_{q-k})\sigma^2, & k = 1, 2, \cdots, q \\ 0, & k > q \end{cases} \end{aligned} $$
From this we can find the autocorrelation function for lag $k$:
$$ \rho_X(k) = \begin{cases} \frac{\theta_k + \theta_{k+1}\theta_1 + \theta_{k+2}\theta_2 + \cdots + \theta_q\theta_{q-k}}{1 + \theta_1^2 + \theta_2^2 + \cdots + \theta_q^2}, & k = 1, 2, \cdots, q \\ 0, & k > q \end{cases} $$
To summarize the differences between the two models:
| Model | ACF | PACF |
|---|---|---|
| AR(1) | Tail off | Cut off after lag 1 |
| AR(p) | Tail off | Cut off after lag $p$ |
| MA(1) | Cut off after lag 1 | Tail off |
| MA(q) | Cut off after lag $p$ | Tail off |
Invertibility
We’re interested in expressing an MA series as an AR series. AR series are more intuitive because $X_t$ is a linear combination of the past data, and the AR coefficients can be directly interpreted.
Under certain conditions, we can invert an MA series to an AR series. Taking a zero-mean MA(1) series as an example:
$$ X_t = Z_t + \theta Z_{t-1}, \quad Z_0 = 0 $$
$$ \begin{aligned} X_1 &= Z_1 + \theta Z_0 = Z_1 \\ X_2 &= Z_2 + \theta Z_1 = Z_2 + \theta X_1 \Rightarrow Z_2 = X_2 - \theta X_1 \\ X_3 &= Z_3 + \theta Z_2 = Z_3 + \theta(X_2 - \theta X_1) = Z_3 + \theta X_2 - \theta^2 X_1 \\ &\,\vdots \\ X_t &= Z_t + \theta Z_{t-1} = Z_t + \theta X_{t-1} - \theta^2 Z_{t-2} \\ &= \cdots = Z_t + \theta X_{t-1} - \theta^2 X_{t-2} + \cdots - (-\theta)^k X_{t-k} - (-\theta)^{k+1} \underbrace{Z_{t-k-1}}_{\rightarrow Z_0} \end{aligned} $$
By repeated substitutions,
$$ Z_t = X_t + (-\theta) X_{t-1} + (-\theta)^2 X_{t-2} + \cdots + (-\theta)^k X_{t-k} + \cdots \quad \text{if } |\theta| < 1 $$
The above is not always possible. For example, if $\theta > 1$, the current value will be heavily dependent on data faraway in the past, which doesn’t make sense in a time series. Late we’ll explain how to find this condition systematically.
The current $Z_t$ (shock) is a linear combination of the present and past $X_t$ (returns). Since the remote value $X_{t-j}$ should have very little impact on the current shock, $|\theta| < 1$. Such an MA(1) model is said to be invertible.
Instead of checking stationarity, we usually check invertibility for MA series. The invertibility assures the uniqueness of the connection between values of $\theta$ and $\rho(1)$ in MA(1) - for any value of $\theta$, the reciprocal $\frac{1}{\theta}$ gives the same value for
$$ \rho(1) = \frac{\theta}{1 + \theta^2} = \frac{\frac{\theta}{\theta^2}}{\frac{1 + \theta^2}{\theta^2}} = \frac{\frac{1}{\theta}}{1 + \frac{1}{\theta^2}} $$
Generally, an MA model is invertible if it’s equivalent to a converging infinite order AR model, where converging means that the AR coefficients decrease to 0 as we move back in time.
R code for simulating the MA(1) series.
↩︎1 2 3 4 5set.seed(1) x <- arima.sim(model = list(ma = 0.7), n = 200, rand.gen = rnorm) plot_time_series(x, x_type = "MA(1)")
| Sep 12 | ARMA Model | 8 min read |
| Aug 28 | Autoregressive Series | 9 min read |
| Nov 17 | Spectral Analysis | 9 min read |
| Nov 02 | Decomposition and Smoothing Methods | 14 min read |
| Sep 14 | Model Fitting and Forecasting | 15 min read |
 Yi's Knowledge Base
Yi's Knowledge Base