Definitions in Arbitrary Linear Space
Certain definitions from plane and solid geometry can be extended in a natural way to an arbitrary linear space and can be otherwise generalized, as is now discussed.
Inner product
The inner product or dot product is a function that multiplies vectors together into a scalar. The inner product between two vectors is defined as
$$ \langle \boldsymbol{u},\boldsymbol{v} \rangle = \boldsymbol{u} \cdot \boldsymbol{v} = \boldsymbol{u}^\prime \boldsymbol{v} = \boldsymbol{v}^\prime \boldsymbol{u} = \sum_{i=1}^p u_i v_i $$
where $\boldsymbol{u} \in V$, $\boldsymbol{v} \in V$ and $V$ is a subspace in $\mathbb{R}^p$. Some properties of the inner product are:
- $\boldsymbol{u} \cdot \boldsymbol{u} \geq 0$, and $\boldsymbol{u} \cdot \boldsymbol{u} = 0 \Leftrightarrow \boldsymbol{u} = \boldsymbol{0}$.
- $\boldsymbol{u} \cdot \boldsymbol{v} = \boldsymbol{v} \cdot \boldsymbol{u}$.
- $(\boldsymbol{u} + \boldsymbol{v}) \cdot \boldsymbol{w} = \boldsymbol{u} \cdot \boldsymbol{w} + \boldsymbol{v} \cdot \boldsymbol{w}$.
- $(c\boldsymbol{u}) \cdot \boldsymbol{v} = c(\boldsymbol{u} \cdot \boldsymbol{v})$.
Norm
The norm of a vector measures the “size” of a vector. Any function that satisfies the following conditions is considered a norm:
- $\|\boldsymbol{u}\| \geq 0$.
- $\|\boldsymbol{u}\| = 0$ if $\boldsymbol{u} = \boldsymbol{0}$.
- $\|\alpha \boldsymbol{u}\| = |\alpha| \|\boldsymbol{u}\|$.
- $\|\boldsymbol{u} + \boldsymbol{v}\| \leq \|\boldsymbol{u}\| + \|\boldsymbol{v}\|$.
In this class, we specifically use the Euclidean norm ($L_2$ norm), which is defined as
$$ \|\boldsymbol{u}\|_2 = \sqrt{\boldsymbol{u} \cdot \boldsymbol{u}} = \sqrt{\sum_{i=1}^n u_i^2} $$
Another commonly used norm is the $L_1$ norm, which is
$$ \|\boldsymbol{u}\|_1 = \sum_{i=1}^n |u_i| $$
In general, the $L_p$ norm is defined as
$$ \|\boldsymbol{u}\|_p = \left(\sum_{i=1}^n |u_i|^p \right)^\frac{1}{p} $$
and the norms for $0 \leq p \leq 2$ are extensively studied. The sup-norm is
$$ \|\boldsymbol{u}\|_\infty = \max_{1 \leq i \leq n} |u_i| $$
and finally the $L_0$ norm is
$$ \|\boldsymbol{u}\|_0 = \text{ # of non-zero elements} $$
Using the vector $\boldsymbol{u} - (1, 0, 3, -4)^\prime$ as an example, the norms are
$$ \begin{aligned} &\|\boldsymbol{u}\|_2 = \sqrt{1 + 9 + 16}, &&\|\boldsymbol{u}\|_1 = 1 + 3 + 4, \\ &\|\boldsymbol{u}\|_\infty = 4, &&\|\boldsymbol{u}\|_0 = 3 \end{aligned} $$
Distance
The distance between two vectors is denoted $d(\boldsymbol{u}, \boldsymbol{v})$, and has to satisfy the following conditions:
- $d(\boldsymbol{u}, \boldsymbol{v}) \geq 0$.
- $d(\boldsymbol{u}, \boldsymbol{v}) = 0$ if and only if $\boldsymbol{u} = \boldsymbol{v}$.
- $d(\boldsymbol{u}, \boldsymbol{v}) = d(\boldsymbol{v}, \boldsymbol{u})$.
- Triangular inequality: $d(\boldsymbol{u}, \boldsymbol{w}) \leq d(\boldsymbol{u}, \boldsymbol{v}) + d(\boldsymbol{v}, \boldsymbol{w})$.
The Euclidean distance ($L_2$ distance) is the most common choice:
$$ \|\boldsymbol{u} - \boldsymbol{v}\|_2 = \sqrt{\sum_{i=1}^n (u_i - v_i)^2} $$
It has a very natural interpretation: imagine a line connecting the two endpoints of the vectors. The $L_2$ distance is the length of this line1.
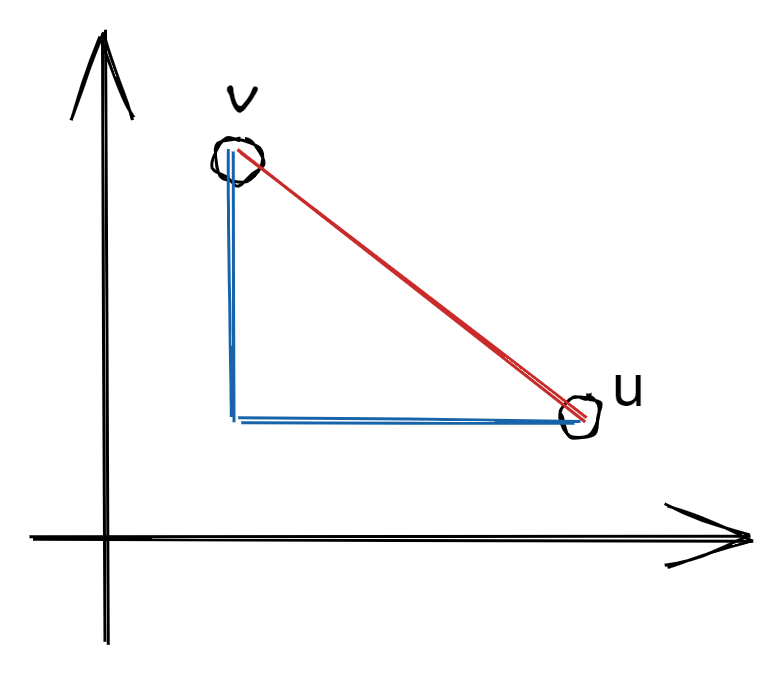
Triangular inequality
Let’s see if the $L_2$ norm satisfies the triangular inequality:
$$ \|\boldsymbol{u} + \boldsymbol{v}\|_2 \leq \|\boldsymbol{u}\|_2 + \|\boldsymbol{v}\|_2 $$
As both sides are $\geq 0$, we will prove
$$ \|\boldsymbol{u} + \boldsymbol{v}\|_2^2 \leq \left(\|\boldsymbol{u}\|_2 + \|\boldsymbol{v}\|_2 \right)^2 $$
$$ \begin{gathered} LHS = \sum_{i=1}^n (u_i + v_i)^2 = \sum u_i^2 + \sum v_i^2 + 2 \sum u_i v_i = \|\boldsymbol{u}\|^2 + \|\boldsymbol{v}\|^2 + 2\boldsymbol{u}\cdot\boldsymbol{v} \\ RHS = \|\boldsymbol{u}\|^2 + \|\boldsymbol{v}\|^2 + 2 \|\boldsymbol{u}\| \|\boldsymbol{v}\| \end{gathered} $$
Thus we need to prove $\|\boldsymbol{u}\| \|\boldsymbol{v}\| \geq \boldsymbol{u} \cdot \boldsymbol{v}$. If $\boldsymbol{u} \cdot \boldsymbol{v} < 0$, the inequality is obvious. When $\boldsymbol{u} \cdot \boldsymbol{v} \geq 0$, we may use the Cauchy-Schwarz inequality:
$$ (\boldsymbol{u} \cdot \boldsymbol{v})^2 \leq \|\boldsymbol{u}\|^2 \|\boldsymbol{v}\|^2 $$
The “high-school” version of this is
$$ (ax + by)^2 \leq (a^2 + b^2)(x^2 + y^2) $$
This is a special case with $\boldsymbol{u} = (a, b)^\prime$ and $\boldsymbol{v} = (x, y)^\prime$. The equality happens when $bx = ay$, i.e. $\boldsymbol{u} \propto \boldsymbol{v}$.
In terms of real numbers, Cauchy-Schwarz tells us that
$$ \left(\sum u_iv_i \right)^2 \leq \left(\sum u_i^2 \right) \left(\sum v_i^2 \right) $$
The geometric interpretation of this is as follows.
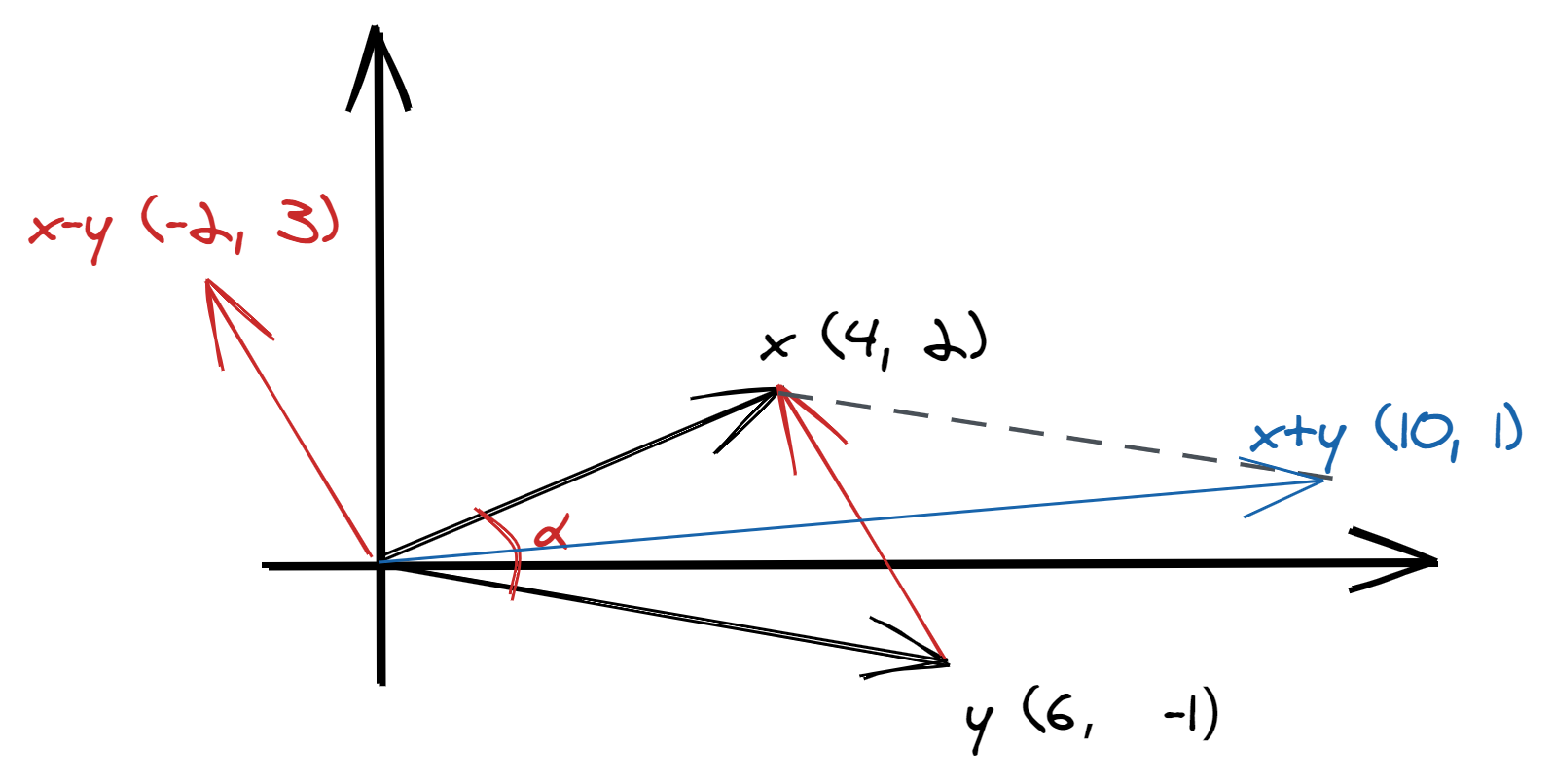
The law of cosine tells us that
$$ \begin{aligned} \|\boldsymbol{x} - \boldsymbol{y}\|^2 &= \|\boldsymbol{x}\|^2 + \|\boldsymbol{y}\|^2 - 2\|\boldsymbol{x}\| \|\boldsymbol{y}\| \cos(\alpha) \\ \|\boldsymbol{x} - \boldsymbol{y}\|^2 &= (\boldsymbol{x} - \boldsymbol{y})^\prime(\boldsymbol{x} - \boldsymbol{y}) \\ &= \|\boldsymbol{x}\|^2 + \|\boldsymbol{y}\|^2 - 2\boldsymbol{x}^\prime \boldsymbol{y} \\ \Rightarrow \boldsymbol{x}^\prime\boldsymbol{y} &= \|\boldsymbol{x}\| \|\boldsymbol{y}\| \cos(\alpha) \end{aligned} $$
We get
$$ \cos(\alpha) = \frac{\boldsymbol{x}^\prime \boldsymbol{y}}{\|\boldsymbol{x}\| \|\boldsymbol{y}\|} $$
In our example figure above, we can find $\cos(\alpha) = \frac{24-2}{\sqrt{20}\sqrt{37}}$.
As $-1 \leq \cos(\alpha) \leq 1$,
$$ \begin{gathered} -1 \leq \frac{\boldsymbol{x}^\prime \boldsymbol{y}}{\|\boldsymbol{x}\| \|\boldsymbol{y}\|} \leq 1 \\ 0 \leq \left(\frac{\boldsymbol{x}^\prime \boldsymbol{y}}{\|\boldsymbol{x}\| \|\boldsymbol{y}\|} \right)^2 \leq 1 \\ (\boldsymbol{x}^\prime \boldsymbol{y})^2 \leq \|\boldsymbol{x}\|^2 \|\boldsymbol{y}\|^2 \end{gathered} $$
which is the Cauchy-Schwarz inequality. The equality happens when $\alpha = 0$. If $\alpha = 90^\circ$, $\cos(\alpha) = 0$ and $\boldsymbol{x}^\prime \boldsymbol{y} = 0$.
What about $\boldsymbol{x} + \boldsymbol{y}$?
$$ \begin{aligned} \|\boldsymbol{x} + \boldsymbol{y}\|^2 &= (\boldsymbol{x} + \boldsymbol{y})^\prime (\boldsymbol{x} + \boldsymbol{y}) \\ &= \|\boldsymbol{x}\|^2 + \|\boldsymbol{y}\|^2 + 2 \boldsymbol{x}^\prime \boldsymbol{y} \\ &= \|\boldsymbol{x}\|^2 + \|\boldsymbol{y}\|^2 + 2\|\boldsymbol{x}\| \|\boldsymbol{y}\| \cos(\alpha) \end{aligned} $$
If $\alpha = 90^\circ$, $\|\boldsymbol{x} + \boldsymbol{y}\|^2 = \|\boldsymbol{x}\|^2 + \|\boldsymbol{y}\|^2$.
Orthogonality
For vectors $\boldsymbol{u}, \boldsymbol{v} \in \mathbb{R}^n$, we say they are orthogonal if
$$ \boldsymbol{u} \cdot \boldsymbol{v} = \langle \boldsymbol{u}, \boldsymbol{v} \rangle = \boldsymbol{u}^T\boldsymbol{v} = \sum_{i=1}^n u_i v_i = 0, $$
which is denoted $\boldsymbol{u} \perp \boldsymbol{v}$.
Orthogonal basis
Let a set of non-zero vectors $\{\boldsymbol{u}_1, \cdots, \boldsymbol{u}_n\}$ be a basis for $V$. If $\boldsymbol{u}_i \perp \boldsymbol{u}_j$ for all $i \neq j$, then we say $\{\boldsymbol{u}_1, \cdots, \boldsymbol{u}_n\}$ is an orthogonal basis of $V$.
Corollary: The $\boldsymbol{u}_i$’s are linearly independent. To prove this, we set $\sum \alpha_i \boldsymbol{u}_i = \boldsymbol{0}$. Consider the inner product between $\sum \alpha_i \boldsymbol{u}_i$ and $\boldsymbol{u}_1$:
$$ \begin{aligned} 0 &= \langle \boldsymbol{0}, \boldsymbol{u}_1 \rangle = \langle \sum \alpha_i \boldsymbol{u}_i, \boldsymbol{u}_1 \rangle \\ &= \sum \alpha_i \langle \boldsymbol{u}_i, \boldsymbol{u}_1 \rangle \quad \text{(distributive, associative)} \\ &= \alpha_1 \langle \boldsymbol{u}_1, \boldsymbol{u}_1 \rangle + \alpha_2 \langle \boldsymbol{u}_2, \boldsymbol{u}_1 \rangle + \cdots + \alpha_n \langle \boldsymbol{u}_n, \boldsymbol{u}_1 \rangle \\ &= \alpha_1 \|\boldsymbol{u}_1 \|^2, \end{aligned} $$
which implies either $\alpha_1 = 0$ or $\|\boldsymbol{u}_1 \|^2 = 0$. Here $\alpha_1$ must be zero because we’ve stated all the $\boldsymbol{u}_i$’s are non-zero vectors. Repeat this and replace $\boldsymbol{u}_1$ with $\boldsymbol{u}_2, \cdots, \boldsymbol{u}_n$, we can show that all the $\alpha$’s are zero, which proves linear independence.
Orthogonal bases are not unique. For example, $\mathbb{R}^3$ has
$$ \begin{gathered} \{(1, 0, 0)^\prime, (0, 1, 0)^\prime, (0, 0, 1)^\prime\} \\ \{(1, 1, 0)^\prime, (1, -1, 0)^\prime, (0, 0, 1)^\prime\} \\ \vdots \end{gathered} $$
So how do we make an orthogonal basis from a given non-orthogonal basis? We’ll introduce the method after the next chapter (projection).
Normalization
For any non-zero vector $\boldsymbol{u} \in \mathbb{R}^n$, the normalized vector of $\boldsymbol{u}$ is
$$ \boldsymbol{e} = \frac{\boldsymbol{u}}{\|\boldsymbol{u}\|} = \frac{1}{\|\boldsymbol{u}\|}(\boldsymbol{u}_1, \cdots, \boldsymbol{u}_n) $$
This is also called the unit vector, and the unit norm is 1:
$$\|\boldsymbol{e}\| = \left\| \frac{\boldsymbol{u}}{\|\boldsymbol{u}\|} \right\| = \frac{1}{\|\boldsymbol{u}\|} \cdot \|\boldsymbol{u}\| = 1$$
For example, let $\boldsymbol{u} = (2, 3, -1)^\prime$. the norm of $\boldsymbol{u}$ is
$$ \|\boldsymbol{u}\| = \sqrt{4 + 9 + 1} = \sqrt{14} $$
and the normalized vector is
$$ \boldsymbol{e} = \frac{\boldsymbol{u}}{\|\boldsymbol{u}\|} = \left( \frac{2}{\sqrt{14}}, \frac{3}{\sqrt{14}}, -\frac{1}{\sqrt{14}} \right)^\prime $$
Orthonormal basis consists of normalized, orthogonal vectors.
For the
Manhattan distanceor $L_1$ distance, think of it as travelling from $\boldsymbol{u}$ to $\boldsymbol{v}$ but you can only move horizontally or vertically. ↩︎
| Sep 21 | Projection | 7 min read |
| Aug 31 | Vector Space | 8 min read |
| Oct 12 | Matrix Inverse | 6 min read |
| Sep 30 | Linear Space of Matrices | 7 min read |
| Sep 28 | Orthogonalization | 5 min read |
 Yi's Knowledge Base
Yi's Knowledge Base